Si la théorie de Newton
rendait bien compte des mouvements des astres, encore fallait-il confirmer
par l'expérience la loi de force gravitationnelle, chose impossible
au XVIIe siècle puisque les masses des planètes et la constante
de gravitation G n'étaient pas connues. C'est ce que réalisa
en 1798 le physicien anglais Henry Cavendish. Son dispositif, destiné
à déterminer la densité de la Terre, permit de mesurer
l'attraction gravitationnelle de 2 sphères métalliques sur
2 billes de plomb fixées aux bouts d'une tige de bois suspendue
à un fil. L'attraction dévie le pendule d'un petit angle ,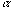
dont la valeur est proportionnelle à l'intensité de la force.
Connaissant la masse des boules, on put en déduire G (dont la valeur
vaut  ).
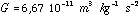Olivier Néron de Surgy, rédacteur en chef adjoint de Sciences
et Avenir . |
Afin de prouver que la Lune n'est
pas une sphère parfaite, Galilée fit remarquer que si c'était
le cas, seuls les rayons du Soleil réfléchis en un point
de sa surface pourraient revenir vers nous, les autres étant réfléchis
dans d'autres directions ; on ne la verrait donc pas. Comme la Lune, les
sphères que nous observons dans la vie courante sont bien visibles,
car leurs surfaces ne sont pas lisses. Galilée affirma en outre
que les tâches maculant la surface lunaire correspondaient à
des montagnes. Par conséquent, la Lune avait une nature terrestre
; elle ne pouvait être constituée d'une quelconque " quintessence
divine ", ainsi que l'imposait la cosmologie d'Aristote. En fait, nous
savons que ces montagnes sont formées par des cratères d'impacts,
Galilée aurait pu s'en servir comme argument pour soutenir que la
chute des corps, dont il donna la loi en 1632 (en un temps t, un corps
subissant l'accélération g parcourt la distance  ),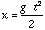
peut aussi bien s'appliquer sur la Lune. Ce que Galilée affirme
surtout avec cette loi, c'est que la nature est écrite en langage
mathématique, et que ce langage est tant celui de la physique terrestre
que celui de la cinématique céleste. La perfection du cosmos
se rencontre dans la matérialité physique elle-même.
Jean-Jacques Szczeciniarz, philosophe historien des sciences. Professeur
à l'université de Bordeaux III . |
Lancez une pomme devant vous. Pendant
sa chute vers le sol, la pomme est en orbite autour du centre de la Terre,
comme la Lune est en orbite autour de la Terre. Elle tombe comme si toute
la masse de la Terre était au centre de celle-ci ; elle passerait
alors tout près de son centre, atteindrait les antipodes, repasserait
près du centre et reviendrait dans votre dos avec la vitesse que
vous lui avez imprimée. On peut décrire la chute d'une pomme
comme une succession de déplacements rectilignes infinitésimaux,
dont une composante est tangente à son orbite (selon le principe
d'inertie, un corps non soumis à une force extérieure conserve
un mouvement rectiligne uniforme), l'autre composante étant dirigée
vers le centre de la Terre (à cause de la force d'attraction gravitationnelle).
L'elliptique d'une orbite peut donc être approchée par un
très grand nombre de petits mouvements rectilignes ; c'est ainsi
que Newton a décomposé le mouvement de la Lune pour montrer
qu'elle chutait perpétuellement sur la Terre sans jamais l'atteindre,
puis déduit la relation entre la force d'attraction gravitationnelle 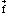 et
l'accélération de la pesanteur  ,
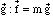où m est la masse du corps qui subit cette accélération.
Jean-Jacques Szczeciniarz, philosophe historien des sciences. Professeur
à l'université de Bordeaux III .
|
| La loi de la gravitation universelle établie
par Newton dans les années 1680 permit de calculer les mouvements
des planètes et des satellites du système solaire avec une
grande précision, grâce aux méthodes analytiques développées
notamment par les mathématiciens français Louis de Lagrange
et Pierre Simon de Laplace, dès la fin du XVIIIe siècle.
En 1915, cette loi fut quelque peu modifiée par la théorie
de la relativité générale d'Albert Einstein : les
mouvements des corps n'y sont plus décrits comme résultant
de forces gravitationnelles entre les corps massifs, mais comme conséquences
des déformations de l'espace-temps déterminées par
la distribution de la matière. Cette refonte théorique fut
immédiatement confirmée par le fait qu'elle rendait bien
compte des différences entre les variations observées de
l'orbite de Mercure et les variations calculées à partir
des équations de Newton. Puis en 1919, lors d'une éclipse
de Soleil, l'observation d'une étoile permit de constater que les
rayons lumineux étaient légèrement déviés
au voisinage du Soleil, ce qui rendait compte de la courbure de l'espace-temps.
Olivier Néron de Surgy, rédacteur en chef adjoint de Sciences
et Avenir . |